1. 스택: 한 쪽 끝에서만 자료를 넣고 뺄 수 있는 LIFO(Last In First Out) 형식의 자료 구조
- 후입선출 (LIFO : Last-In First-Out) 방식 먼저 들어 온 것이 아래에 있으므로 나중에 들어온 것이 먼저 사용 또는 제거되는 특징을 가짐. (반대 개념 FIFO : First-In First-Out

2. Push/Pop 함수
- Push 함수 : 스택에 값을 넣을 때(제일 상단에 값을 추가/삽입 함)
- Pop 함수 : 스택에서 값을 꺼낼 때(제일 상단의 값을 추출/삭제)

3. 스택의 구현 방식
배열 방식 (주로 사용하는 방식)
- 단순한 배열 또는 객체의 배열을 사용
- 배열 인덱스(스택포인터)를 이용하여 편리하게 사용
- 배열(스택) 크기에 제한 존재 -> 수시 확인 필요
연결리스트 방식
- 노드/연결리스트 방식으로도 구현 가능
- 스택 크기에 제한이 없음
- 일반적으로 연결리스트는 원소 삽입/삭제시 매우 유리하나, 스택의 경우, 배열 방식보다 다소 복잡한 면이 있어, 배열 방식을 선호
4. 스택 관련 주요 연산/ 함수
• createStack() ::= 스택을 생성한다.
• is_empty(s) ::= 스택 s가 비어있는지를 검사한다.
• is_full(s) ::= 스택 s가 가득 찼는지를 검사한다. (배열인 경우)
• push(s, e) ::= 스택 s의 맨 위에 요소 e를 추가한다.
• pop(s) ::= 스택 s의 맨 위에 있는 요소를 삭제한다.
• peek(s) ::= 스택 s의 맨 위에 있는 요소를 삭제하지 않고 반환한다
5. 스택의 용도
- 입력 순서의 역순으로 자료를 출력하고자 할 때

- 함수 호출시 복귀 주소 저장, 특히 재귀함수(recursion)
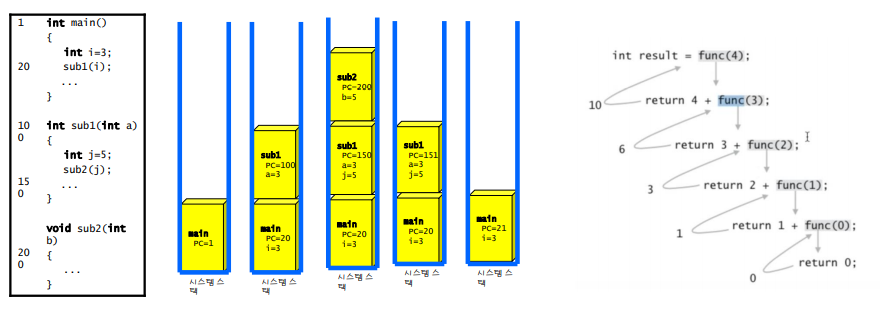
- 수식 계산(후위 표기 변경 및 연산)

6. 스택의 구현 (배열)
- 배열의 인덱스 이용
•첫 자료를 stack[0], 다음 자료를 stack[1]에 넣는 방식
- 스택 포인터(stack pointer)라는 변수를 사용
• 가장 마지막 자료의 배열 인덱스를 저장
• 주로 sp 또는 top 등의 변수명을 사용하며, 초기값은 주로 -1로 설정
• 원소가 3개 스택에 들어있다면, 즉, stack[0], stack[1], stack[2]에 자료가 있으므로, top = 2로 설정
• 항상 첫 원소는 stack[0], 마지막 원소는 stack[top]에 저장됨
- 스택 포인터(인덱스)의 값으로 원소 개수 추정도 가능
예) top 값이 -1이면, 그 스택은 비어 있음.
예) top = 2이면, 3개의 원소를 보유
- 배열 방식의 스택은 배열을 세워서 설명하는 경우가 많음
7. 구현 (배열)
#include <iostream>
using namespace std;
// 객체 선언 방식 스택의 기본 함수 구현, 몇가지 간이 테스트
#define element int
//#define MAX_SIZE 100
const int MAX_SIZE = 100;
/*
**************************객체방식 + 배열**************************
class Stack {
public:
element MyStack[MAX_SIZE];
int top;
Stack() {
top = -1;
}
bool is_stack_empty() {
return(top == -1);
}
bool is_stack_full() {
return (top == MAX_SIZE - 1);
}
void push(element data) {
if (is_stack_full()) {
cout << "ERROR: Stack FUll" << endl;
return;
}
else {
MyStack[++top] = data;
}
}
element pop() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1;
}
else {
return MyStack[top--];
}
}
element peek() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1;
}
else {
return MyStack[top]; //***
}
}
void print_stack() {
cout << "STACK STATUS (top = " << top << " )" << endl;
if (is_stack_empty()) return;
else {
for (int i = top; i >= 0; i--)
cout << MyStack[i] << endl;
}
}
};
void main() {
Stack MyTT;
MyTT.push(10); //MyTT라는 객에서 push
MyTT.push(20);
MyTT.push(30);
MyTT.pop();
MyTT.pop();
MyTT.push(40);
MyTT.push(50);
MyTT.pop();
MyTT.push(60);
MyTT.print_stack();
}
*/
element Stack[MAX_SIZE];
int top = -1; // 초기화(아직 바깥쪽을 나타내고 있음). sp = -1
bool is_stack_empty() {
//if (top == -1) return true;
//else return false;
return(top == -1); //조건식 리턴. ***
}
bool is_stack_full() {
//if (top == MAX_SIZE - 1) return true;
//else return false;
return (top == MAX_SIZE - 1);
}
void push(element data) {
if (is_stack_full()) {
cout << "ERROR: Stack FUll" << endl;
return;
}
else {
//top++;
//Stack[top] = data;
Stack[++top] = data; //Stack[topp++] = data;과의 차이 이해하기. 식을 실행 한 다음 더하라.
}
}
element pop() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1; // exit(); pop과 push는 리턴값을 정해주어야한다.
}
else {
//element x = Stack[top]; //가장 상단에 있는 것을 저장한다.
//top--; //제일 위에 있는것 보다 하나 아래쪽을 가리키도록 한다.
//return x; // 아까 저장한 x 리턴.
return Stack[top--]; //top을 바꾸기 전 값으로 리턴. 그리고 바로 top의 값을 바꾼다.***
}
}
element peek() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1;
}
else {
return Stack[top]; //***
}
}
void print_stack() {
cout << "STACK STATUS (top = " << top << " )" << endl;
if (is_stack_empty()) return;
else {
for (int i = top; i >= 0; i--)
cout << Stack[i] << endl;
}
}
void main() {
push(10);
push(20);
push(30);
pop();
print_stack();
push(40);
push(50);
pop();
push(60);
print_stack();
}
8. 스택의 구현 (연결리스트)
• 권장하지 않는 방법
- push, pop만 사용하므로 삽입, 삭제 시 별 다른 이점이 없음
- 구현이 복잡함.
• 장점: 스택 크기가 제한되지 않는다.
* 연산 수행과정
1) 공백 스택 생성 createStack();

2) 원소 A 삽입 push(stack, A);

3) 원소 B 삽입 push(stack, B);

4) 원소 C 삽입 push(stack, C);

5) 원소 삭제 pop(stack)

9. 구현 (연결리스트)
#include <iostream>
using namespace std;
//연결리스트를 이용한 스택의 기본 함수 구현, 몇가지 테스트.
#define element int
class Node {
public:
element data;
Node* link;
};
Node* SP = NULL; //Stack Pointer
bool is_stack_empty() {
return(SP == NULL);
}
//is_stack_full이라는 함수 존재하지 않는다.
void push(element data) {
//새로운 노드를 첫 노드로 추가
Node *new_node = new Node;
new_node->data = data;
//new_node->link = NULL;
new_node->link = SP;
SP = new_node;
}
element pop() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1; //exit();
}
else {
element item = SP->data;
SP = SP->link;
return item;
}
}
element peek() {
if (is_stack_empty()) {
cout << "ERROR: Stack Empty" << endl;
return -1; //exit();
}
else {
return SP->data;
}
}
void print_stack() {
cout << "STACK STATUS" << endl;
if (is_stack_empty()) return;
else {
for (Node* ptr = SP; ptr != NULL; ptr = ptr->link)
cout << ptr->data << endl;
}
};
void main() {
push(10);
push(20);
push(30);
pop();
print_stack();
push(40);
push(50);
pop();
push(60);
print_stack();
}
'ⓢⓣⓤⓓⓨ > 자료구조' 카테고리의 다른 글
| [자료구조] 큐 (0) | 2021.07.05 |
|---|---|
| [자료구조] 연결리스트 (0) | 2021.05.20 |
| [자료구조] 문자열과 포인터, 구조체, 객체와 포인터 (4) | 2021.05.10 |



댓글